如果暴力法求2的平方根,应该是二分查找,不断的用中点的平方与2进行对比,然后根据对比结果改变查找结果的范围。
这种方法如果要求精确度比较高的时候,查找的次数将非常可观。该算法暂且不在本文讨论。
本文要讨论的是一种可以快速求解函数零点的算法-牛顿迭代,可以用在求2的平方根上。
此牛顿即科学之父,艾萨克·牛顿。
求2的平方根,其实就是求 f(x) = x² – 2函数,当f(x)=0时x的解。
如何找到这个x的值,在牛顿迭代算法中的方法是随机选择曲线f(x)上的一个点。
假设第一个选取的是(x₀, y₀) = (4, 14)。
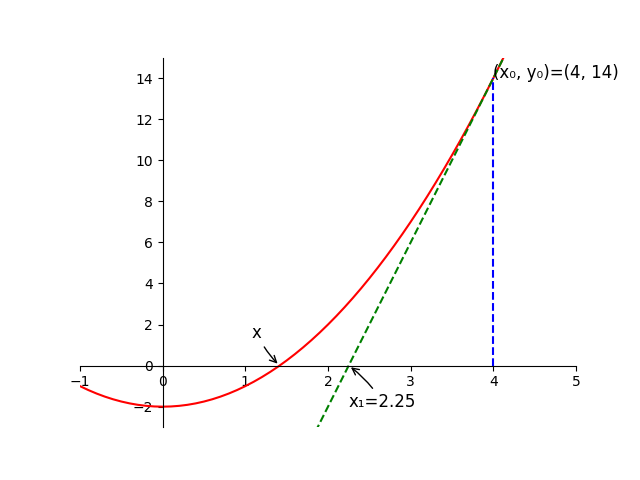
如图1可以看出该点的切线与x轴的交点(x₁, 0)是一个更加接近(x, 0)的值。
那么如何求x₁的值,我们需要求切线的函数。
切线是一条直线,已知该切线经过(x₀, y₀),(x₁, 0)两点,且切线的斜率为2x₀(斜率的推导先搁置,文末会详细推导)。
所以,可得
0-y₀ = (x₁ – x₀)*2x₀
x₁ = x₀ – y₀/(2x₀)
x₁= x₀ – (x₀² – 2)/2x₀
因为x₀=4, 所以x₁= 4 – 14/(2*4) = 2.25
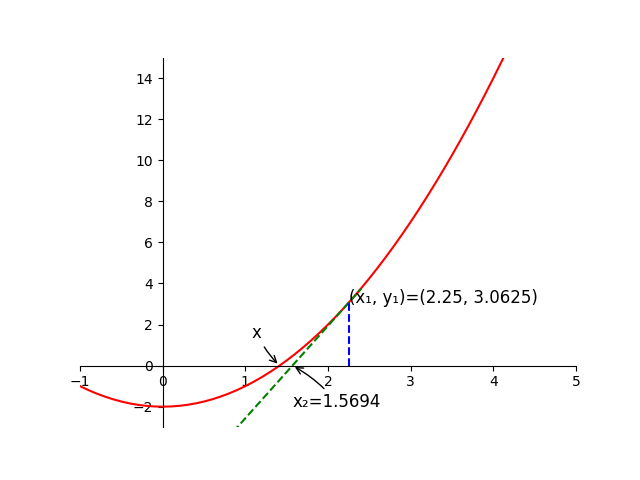
如图2
在(x₁, 0)作一条垂直x轴的直线与f(x)曲线的交点为(x₁, y₁),
则(x₁, y₁)点的切线与x轴的交点为(x₂, 0)。
(x₂, y₂)点的切线与x轴的交点为(x₃, 0)。
(x₃, y₃)点的切线与x轴的交点为(x₄, 0)。
……
所以整个迭代过程如下:
x₀=4.0000000000
x₁=2.2500000000
x₂=1.5694444444
x₃=1.4218903638
x₄=1.4142342859
x₅=1.4142135625
x₆=1.4142135624
……
随着不断迭代,切线交点不断向x接近,最终可以得到一个x的近似值,当达到一定的精确度之后,迭代停止。
此迭代思路亦可应用于其他函数零点的求解中,只需改变对应的曲线和切线的函数即可。
Java代码实现,递归实现
public class Newton {
public static void main(String[] args) {
double x = newton(2);
}
private static double newton(double x) {
if (Math.abs(x * x - 2) > 0.0000000001) { // 精确度达到小数点后10位停止迭代
return newton(x - (x * x - 2) / (2 * x));
} else {
return x;
}
}
}
附录
f(x) = x² – 2 函数曲线的切线斜率的推导
需要使用微积分的思维
我们知道曲线上两点(x₀, y₀)(x₁, y₁)连线的斜率的求解方法为
(y₀-y₁)/(x₀ – x₁)
y₀=x₀² – 2
y₁=x₁² – 2
代入斜率计算公式 = ((x₀² – 2) – (x₁² – 2))/(x₀ – x₁)
=(x₀² – x₁²)/(x₀ – x1)
=(x₀ – x₁)*(x₀ + x₁)/(x₀ – x₁)
=x₀ + x₁
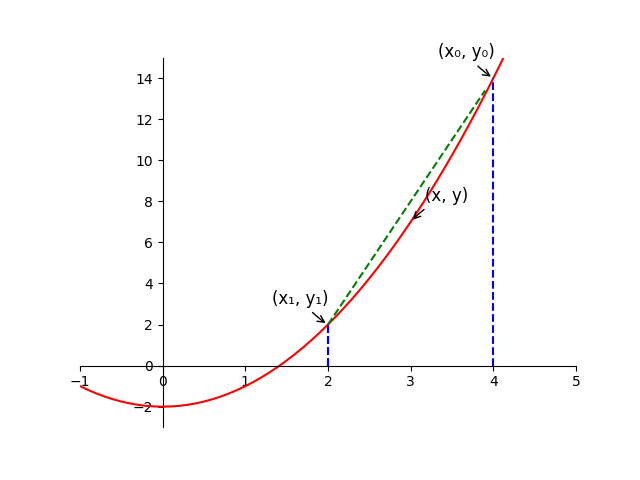
当(x₀, y₀)(x₁, y₁)无限接近(x, y)时的直线的斜率即为该点的切线斜率
lim(x₀ + x₁) = 2x
可求得点(x, y)的切线斜率 = 2x