作者归档：justin

布谷鸟过滤器的简单Java实现

发表评论

布谷鸟过滤器，第一次是在2014年发布的一篇论《Cuckoo Filter: Practically Better Than Bloom》里面提出。
以“布谷鸟”命名，源于该过滤器采用了布谷鸟哈希的思路，而“布谷鸟哈希”算法中的踢出和替换逻辑与布谷鸟的产蛋习性类似。

布谷鸟交配后，雌性布谷鸟就准备产蛋了，但它却不会自己筑巢。它会来到像知更鸟、刺嘴莺等那些比它小的鸟类的巢中，移走原来的那窝蛋中的一个，用自己的蛋来取而代之。– 源自 百度百科

布谷鸟过滤器的数据结构
典型的布谷鸟过滤器是一个4字节一组的二维字节数组buckets，设其数组长度为len，如图1所示。

图1
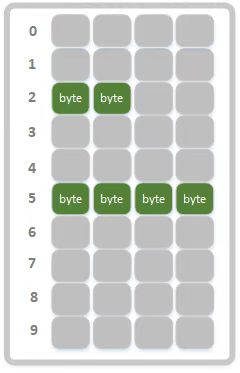
  1. 数组长度根据预估的待过滤样本量和误差率大小决定，当负载因子到达阈值后可进行扩容以避免误差率的上升。（类似HashMap的扩容方式）
  2. 每个bucket连续存储4个字节的由key生成的指纹（后续讲解指纹如何计算），之所以使用这种方式存储是为了充分利用cpu缓存机制。这也是布谷鸟过滤器性能优于布隆过滤器的地方，布隆过滤器多个哈希点位内存分布不连续，导致每次读取点位上的数据都需要查询内存，无法充分利用cpu缓存机制。

布谷鸟过滤器的插入
将key插入过滤器的逻辑分以下主要步骤：

图2
图3
图4
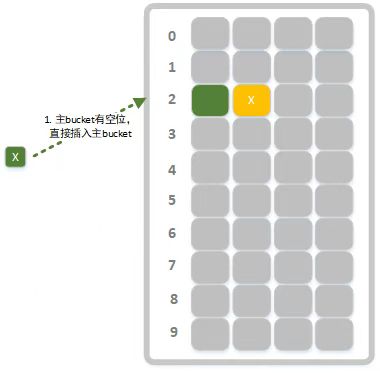
  1. 用哈希算法rsHash()（本文使用RSHash算法, 也可替换为其他哈希算法）计算key的哈希值hash，结合哈希值和buckets的数组长度可得主bucket在buckets中的索引index = hash % len。
  2. 使用指纹算法计算出key的指纹fPrint，常用的取指纹算法为步骤1计算所得hash取最后8位，大小为一个字节。取8位仅为在空间占用和判断准确率之间的一种平衡，最高的准确率肯定是将整个hash值作为指纹，但是空间占用也最大，这种平衡也可以根据实际情况调整。
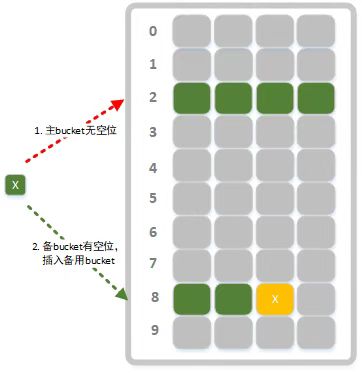
  3. 遍历bucket尝试找到一个空位插入指纹, 如果插入成功则操作完成（如图2所示）。
  4. 如果主bucket无空位则结合指纹fPrint与主bucket索引index计算出备bucket在buckets中的索引backupIndex =  index ^ (rsHash(fPrint) % len) （为何使用XOR操作后面会说明）
  5. 遍历备bucket尝试找到一个空位插入指纹，如果插入成功则操作完成（如图3所示）。
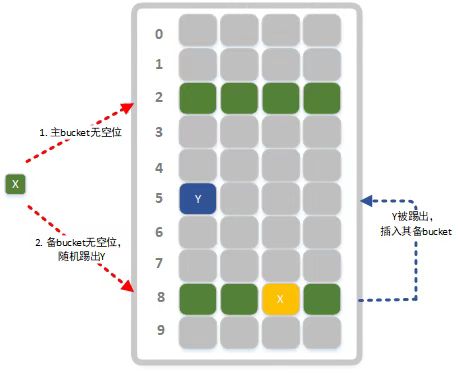
  6. 如果主备bucket都没有空位插入，则随机踢掉主备bucket8个位置上的某个指纹，插入当前指纹。
  7. 被踢出的指纹fPrintOut找寻该指纹对应的另一个bucket插入。当另一个bucket也满，则会继续踢出并插入操作，直到找到空位为止（如图4所示）。
    而被踢出指纹如何快速找到其对应的另一个bucket，则要用到前面提到的^操作。
    由于XOR操作的自反性, a = a ^ b ^ b, 所以
    index = index ^ (rsHash(fPrint) % len) ^ (rsHash(fPrint) % len)
          = backupIndex ^ (rsHash(fPrint) % len)
    主bucket和备bucket可以直接通过XOR操作互相计算得到, 所以当踢出某个指纹时，无需考虑其当前所在的bucket是主bucket还是备bucket，
    直接XOR计算就可以得到对应的另一个bucket的索引，效率会非常高。这也是布谷鸟过滤器设计精妙处之一。

布谷鸟过滤器的查询
过滤器的查询就比较简单，参考前面的插入过程。

  1. 根据key计算指纹和主bucket和备bucket的索引
  2. 遍历主bucket和备bucket，比对指纹和bucket中所有指纹，如果相等，则判断该key可能存在
  3. 遍历完如果不存在相等的指纹，则判断该key一定不存在

布谷鸟过滤器的简单Java实现如下：

主接口方法
私有方法
私有方法

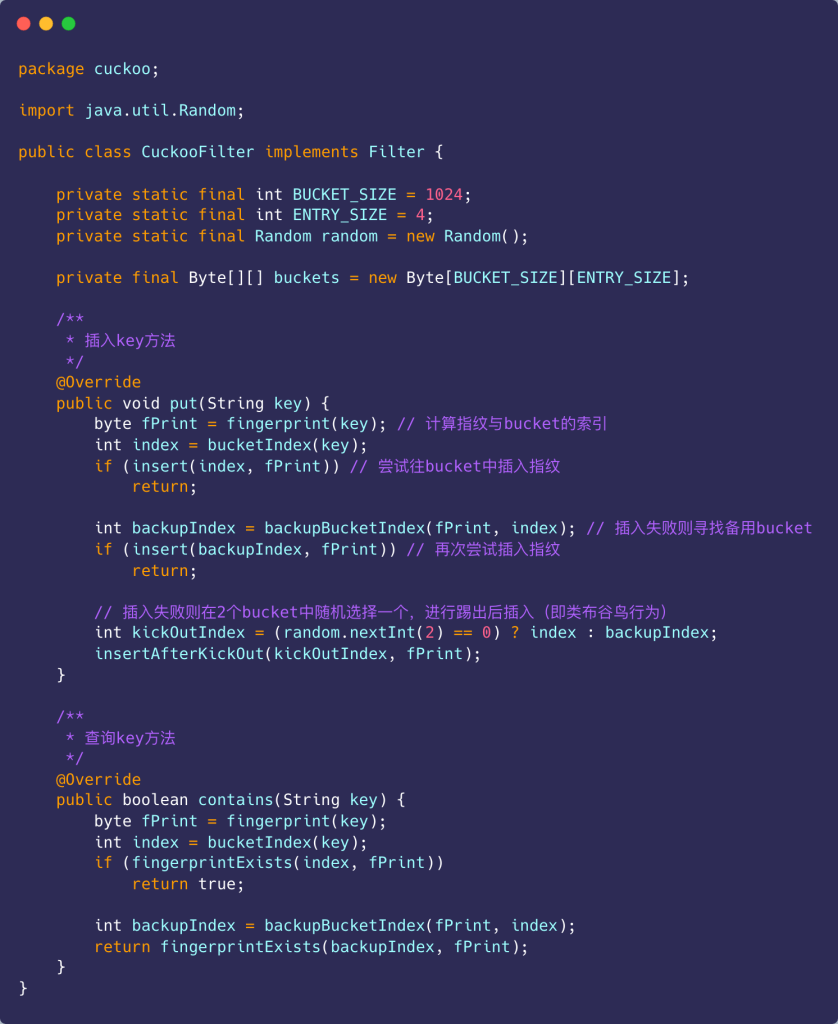
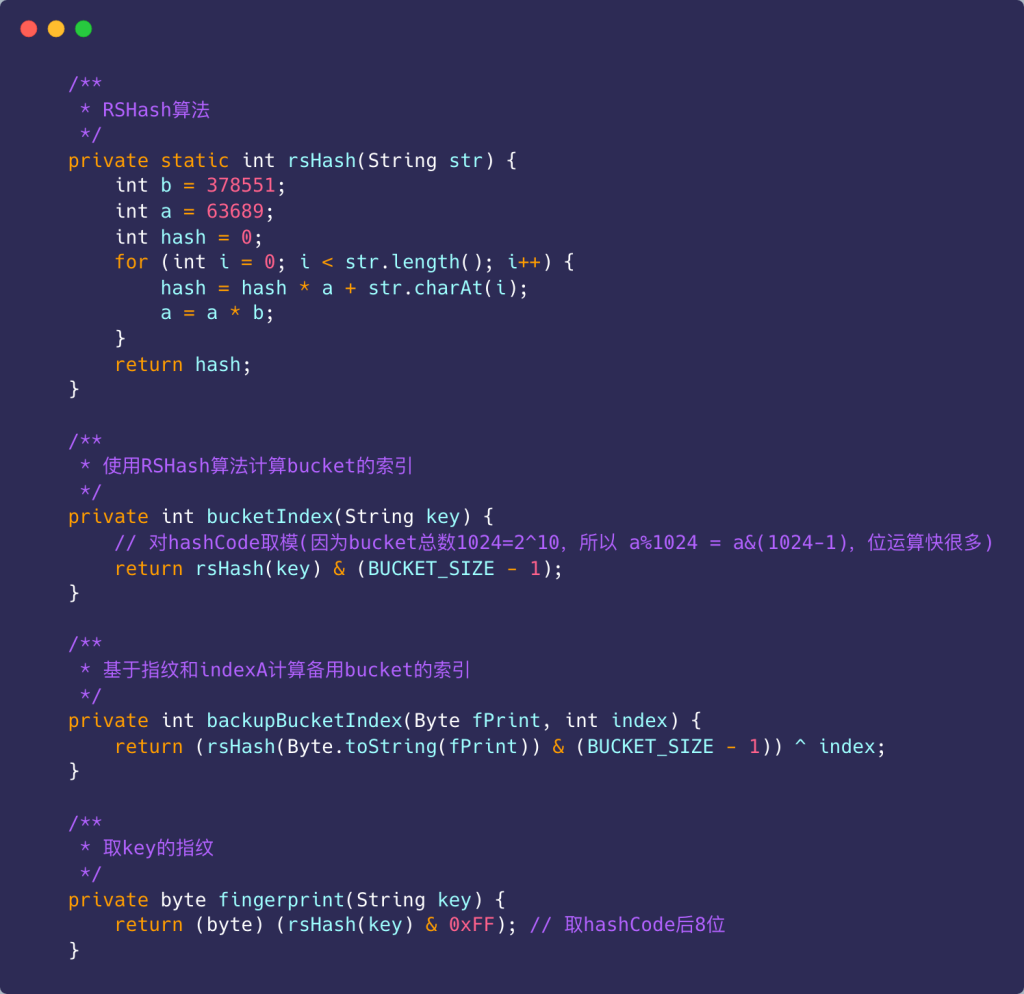
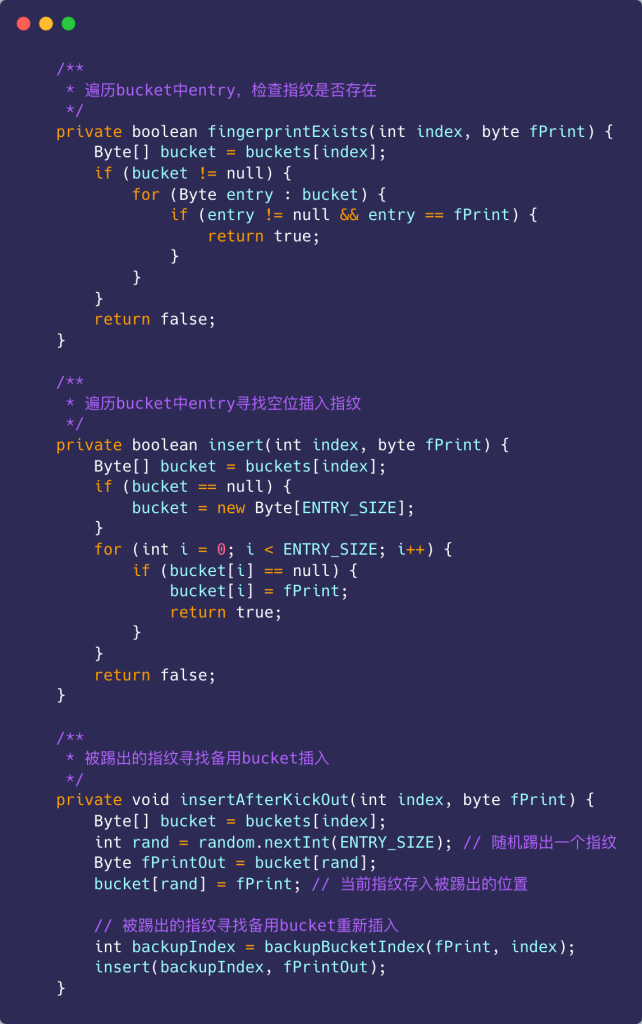
该代码仅实现主要的插入和查询逻辑，待完善部分包含：

  1. 循环踢出和插入处理逻辑
  2. 数组达到负载因子后的扩容处理逻辑
  3. 根据误差率和样本量选择数组容量处理逻辑

附录：

代码请参考: Github地址

本文参考文章链接：
Go语言实现布谷鸟过滤器

RSA加密算法原理

发表评论

RSA加密算法是一种非对称加密算法，也称公开密钥加密。该算法是1977年由Ron Rivest，Adi Shamir和Leonard Adleman三人一起提出的。非对称加密即加密过程会使用一对密钥，公钥和私钥各一个。使用公钥将明文加密成密文，并使用私钥将密文解密成明文。

RSA主要包含两个部分：

  • 公钥和私钥的生成
  • 加密和解密算法

假设Alice要向Bob发送一个RSA加密的报文，其实就是对报文的二进制模式的表现形式所代表的整数进行加密。例如，假设待加密报文的比特模式为1001，其实等价于加密整数9，解密亦然。

公钥和私钥的生成

为了让Alice可以发送加密的密文，Bob需要执行以下步骤生成公钥和私钥：

  1. 选择两个大素数p和q。理论上p和q的乘积越大，则破译的难度越大。目前比较推荐的大小为p和q的乘积为1024比特的数量级。
  2. 计算 n = pq 和 z = (p – 1)(q – 1)
  3. 在小于n的整数中随机选择一个与z互质的整数e，此时公钥生成完成，其中包含n和e，记为K+ = (n, e)。
  4. 求一个数d，满足 ed mod z = 1 即可。此时私钥生成完成，其中包含n和d，记为 K– = (n, d)。

加密和解密算法

Alice要给报文加密时，假设报文的二进制表现形式的整数值为m，且 m < n，使用公钥对m加密的结果为c，则：

c = me mod n

Bob接收到密文后，使用私钥对c进行解密的算法为：

m = cd mod n

RSA的工作原理

通过以上算法为何就能将加密后的密文c解密出原文m呢？在讲解原理之前，首先要引入取模运算的一个重要性质（该性质暂不证明），对于任意值a，n和d都有：

(a mod n)d mod n = ad mod n

将a = me代入该等式则有[等式A]：

(me mod n)d mod n = med mod n

将加密等式 c = me mod n 代入解密函数 f = cd mod n 中可得：

f = (me mod n)d mod n

结合[等式A]，可得：

f = (me mod n)d mod n = med mod n

再引入数论的一个结论（该结论暂不证明）：

如果p和q是素数，且有 n = pq 和 z = (p-1) (q-1) ，则：

xy mod n = x (y mod z) mod n

应用这个结论，将 x = m 和 y = ed 代入等式可得[等式C]：

med mod n = m(ed mod z) mod n

将[等式C]代入函数 f ，可得：

f = med mod n = m(ed mod z) mod n

由前面选取公钥私钥的算法可知 ed mod z = 1，代入函数 f ：

f = m(ed mod z) mod n = m1 mod n = m

最终得出解密函数 f 的结果等于原文m。

RSA的安全性依据

RSA的安全性依赖于目前没有已知的算法可以快速分解一个大数的因数，所以n很难分解出素数p和q。所以根据公钥中已知的n和e，以人类目前计算机的计算能力，需要很多年才能推测出私钥中的d。但是当计算能力极强的量子计算机出现后，RSA的安全性也不是确保的。

Dijkstra最短路径算法

发表评论

戴克斯特拉算法（英语：Dijkstra’s algorithm），又译迪杰斯特拉算法，是由荷兰计算机科学家艾兹赫尔·戴克斯特拉在1956年发明的算法。戴克斯特拉算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题。

算法主要思路如下：

  1. minDist[]记录各节点到A的最短路径，初始化值为整数最大值M=Integer.MAX_VALUE。
  2. visited[]记录各节点的访问情况。
  3. 每次循环选取minDist中路径值最小且未被访问过的节点作为起点，路径值记为min，如果(min+该点到各节点的距离)<minDist记录的最短路径值则更新minDist记录值。
  4. 直到所有节点都被计算完，最终得到A点到各点的最短路径值并返回。

分步骤图示如下：

本文使用二维数组表示图，一维索引表示边的起点，0至5表示A至F节点。二维索引表示边的终点，0至5表示A至F节点。值表示边的长度，无法到达用M最大距离表示。

Java代码实现如下：

点击至Github查看代码

LRU缓存淘汰算法

发表评论

缓存比较常见的一种淘汰策略为LRU(Least Recently Used)，即最近最少使用。其实现原理主要包含以下几点：

  1. HashMap保存Key与缓存节点的映射关系。
  2. 双向链表(Doubly Linked List)保存缓存节点。
  3. 被查询节点移动到链表的尾部。
  4. 当达到缓存最大容量时，移除链表头部节点。

首先实现双向链表节点。

然后实现双向链表。

为何使用双向链表而不是单向链表，因为为保证删除指定节点时可以知道该节点的前置和后置节点，这样才能保证删除节点的时间复杂度为O(1)。从代码可以看出，该链表的新增，弹出和移除节点都达到了O(1)时间复杂度。

最后使用链表和HashMap实现LRU缓存。

保存缓存的HashMap的写入和读取方法以及链表的各方法时间复杂度都为O(1)，所以Cache的写入和读取整体的时间复杂度为O(1)。

测试缓存（最大缓存容量为4）的写入和读取结果如下：

Java实现Ticket, CLH, MCS自旋锁

发表评论

自旋锁(Spinlock)是计算机科学多线程同步的一种锁。线程反复检查锁变量是否可用，使用忙等待的方式保持线程执行。由于自旋锁保持线程执行，避免了进程上下文的调度(该过程操作系统会发生用户态和内核态的切换，开销较大)，所以在锁等待时间较短的场景下，性能上更有优势。

1.简单自旋锁

简单的自旋锁实现一般使用CAS(Compare And Swap)，Java代码如下: public class SimpleLock { private AtomicBoolean flag = new AtomicBoolean(); //锁变量 public void lock() { while (!flag.compareAndSet(false, true)) { //自旋 } } public void unlock() { flag.set(false); } }

这种方式实现的自旋锁的问题是不公平自旋锁，可能会出现线程饥饿问题。

2.Ticket自旋锁

为了实现公平自旋锁，可以模拟银行柜台办理业务的排队叫号机制，就是Ticket自旋锁。

主要思路为：

  1. 线程获取锁之前先获取一个自增长的号(Ticket)。
  2. 等待锁的线程都进入循环等待，检查当前叫号是否等于本线程所获取的号码。
  3. 如果叫号等于本线程获取的号码则获取到锁。
  4. 释放锁时将叫号递增，下一个获取号码等于该叫号的线程继续获取锁。

Java实现Ticket锁代码如下： public class TicketLock { private AtomicInteger ticket = new AtomicInteger(); private AtomicInteger call = new AtomicInteger(); public void lock() { int tick = ticket.getAndIncrement(); //取号 while (tick != call.get()) { //检查叫号和取的号是否相等 //自旋 } } public void unlock() { call.getAndIncrement(); } }

Ticket自旋锁解决了锁公平的问题，先取得号码的线程可以先获取锁(FIFO)。在多CPU计算机中，由于所有竞争锁的线程循环监听一个共享变量call的内存值，为了保证该变量对所有线程都保持可见性，各CPU的缓存会失效，每次循环读取该变量都必须从主存去读取。由于主存的带宽有限，这无疑会产生昂贵的负担。

3.CLH自旋锁

该锁的名称取自其发明人Craig，Landin和Hagersten名字的首字母。该锁采用隐式的链表实现FIFO队列来达到获取锁的公平性。

主要思路为：

  1. 线程获取锁之前新增一个节点node，连接到链表的tail指针后，这样所有等待锁的节点就形成一个队列。
  2. 各等待锁的线程都循环监听前一个节点pre的状态，如果pre的状态为释放锁的状态，则当前线程进入持有锁的状态。
  3. 根据队列FIFO的特性，各线程即可依次获取锁。

CLH自旋锁Java实现如下： public class ClhLock { private AtomicReference<Node> tail; private ThreadLocal<Node> node; private ThreadLocal<Node> pre; public ClhLock() { tail = new AtomicReference<>(new Node()); node = ThreadLocal.withInitial(Node::new); pre = new ThreadLocal<>(); } public void lock() { Node curr = new Node(); //新增node节点 curr.flag = true; //节点设置为待获取锁状态 node.set(curr); Node pr = tail.getAndSet(curr); //读取当前节点的前置节点并将当前节点链接到tail后 pre.set(pr); while (pr.flag){ //检查前置节点的锁状态 //自旋 } } public void unlock() { Node curr = node.get(); curr.flag = false; //当前节点置为未持有锁状态 pre.set(null); //解除前置节点与当前节点的链接 } private class Node { private volatile boolean flag = false; //true=待获取锁或持有锁状态，false=未持有锁状态 } }

CLH锁实现了公平锁，每个线程只循环监听前置节点的锁状态，所以大大降低了内存同步的压力。Java并发包java.util.concurrent中众多锁实现的基础类AbstractQueuedSynchronizer就采用了CLH锁的变体实现，请看JDK1.8源码AbstractQueuedSynchronizer类304行注释： /** * Wait queue node class. * * <p> The wait queue is a variant of a "CLH" (Craig, Landin, and * Hagersten) lock queue. CLH locks are normally used for * spinlocks. We instead use them for blocking synchronizers, but * use the same basic tactic of holding some of the control * information about a thread in the predecessor of its node. **/

CLH锁在对称多处理器（英语：Symmetric Multi-Processing，简称SMP）架构的CPU中运行正常。但是在非统一内存访问架构（英语：Non-uniform Memory Access，简称NUMA）的CPU中会存在频繁访问远端内存的问题，造成性能较差。因为NUMA架构，每个CPU的内存单元都是独立的，本CPU的内存为本地内存，其他CPU的内存为远程内存。而访问远程内存的性能要远远低于访问本地内存。而各等待锁的线程可能同时在不同的CPU上执行，当当前线程监听的前置节点在另一个CPU时，就会频繁的去读取远程内存，这样性能会显著降低。为了解决这个问题，就需要使用MCS自旋锁。

4.MCS自旋锁

该锁的名称依然取自其发明人John Mellor-Crummey和Michael Scott名字的首字母。该锁在CLH锁的基础上做出如下优化：

  1. 等待锁的线程监听本节点的锁状态，如果状态为获得锁，则进入获取锁状态。
  2. 释放锁时修改本节点的后置节点的锁状态。

MCS锁通过自旋监听本节点状态解决了CLH锁在NUMA架构下频繁读取远程内存的性能降低问题，在SMP和NUMA两种架构下都可以获得理想的性能。

MCS自旋锁Java实现如下： public class McsLock { private AtomicReference<Node> tail; private ThreadLocal<Node> node; public McsLock() { tail = new AtomicReference<>(); node = ThreadLocal.withInitial(Node::new); } public void lock() { Node curr = node.get(); Node pre = tail.getAndSet(curr); if (pre != null) { //没有前置节点则当前 pre.next = curr; while (!curr.flag) { //检查当前节点的锁状态 //自旋 } } } public void unlock() { Node curr = node.get(); if (curr.next == null) { //如果当前节点是尾结点，则将尾结点置为null if (tail.compareAndSet(curr, null)) { //由于多线程执行，所以再次检查当前节点是否是尾节点 return; } while (curr.next == null){ //说明当前节点后又新增了节点 } } curr.next.flag = true; //将当前节点的后置节点锁状态置为true curr.next = null; //断开当前节点和后置节点的连接 } private class Node { private volatile boolean flag = false; private volatile Node next; }

浅谈Java中字符串的UTF-8编码格式

发表评论

想探讨Java中字符串的UTF-8编码格式，首先想到的是直接将字符串的字节码打印输出。例如，以下代码试图打印中文”赵”字的UTF-8编码的字节数组。


public class Utf8 {
    public static void main(String[] args) {
        byte[] bts = "赵".getBytes(StandardCharsets.UTF_8);
        System.out.println(Arrays.toString(bts));
    }
}

输出结果如下：

[-24, -75, -75]

输出结果是3个负数，如何理解这个输出结果？

首先，我们知道在Java中，字符串都是使用Unicode(通用字符集)进行编码的。“赵”字在Unicode中的code point(位点)为\u8d75。而本例中UTF-8(8-bit Unicode Transformation Format)是Unicode最常用的一种编码格式。

UTF-8的编码格式规则如下：

代码范围(16进制)二进制编码格式备注
000000 – 00007f0xxxxxxxASCII字符范围，以0开始
000080 – 0007ff110xxxxx 10xxxxxx第1个字节110开始, 第2个字节10开始
000800 – 00D7ff
00e000 – 00ffff
1110xxxx 10xxxxxx 10xxxxxx		第1个字节1110开始，其他字节10开始
010000 – 10ffff11110xxx 10xxxxxx 10xxxxxx 10xxxxxx第1个字节11110开始，其他字节10开始
UTF-8编码格式

编码规则可以看出，UTF-8是一种可变长度字符编码，也是一种前缀码。“赵”的位点16进制8d75，属于3字节的编码规则，所以UTF-8编码格式应该为

1110xxxx 10xxxxxx 10xxxxxx

8d75的二进制表示为

1000 1101 0111 0101

则“赵”的UTF-8编码二进制表示为

11101000 10110101 10110101

Java中对字节进行打印，其实就是将二进制表示的十进制真值输出。而Java中实际存储的是二进制的补码，正数的补码即真值，而负数的补码减1然后取反码即为真值的二进制表示。

因为3个字节第1位符号位(0表示正数，1表示负数)都为1，所以都为负数。则UTF-8编码字节数组的真值应该表示为

10011000 11001011 11001011

最后进行二进制转十进制转换，后7位为数值的绝对值。所以，打印结果为

[-24, -75, -75]

大数据量去重的BitMap解法

发表评论

问题：对一个包含15亿个QQ号的文件进行去重

算法1：数组解法

将QQ号读入内存，组成一个数组。然后遍历这个数组与其他位置比对，如果遇到重复的号码，则表示存在重复。

该算法时间复杂度n^2, 15亿个号码循环次数为(15亿)^2。

所有QQ号码存入内存中，每个QQ号码占用一个整形，一般为32个bit, 空间需要15亿*32个bit约等于5.59G

算法2: HashMap解法

内存中保存一个HashMap, 遍历所有号码，如果HashMap中存在该号码，则表示存在重复。如果不存在该号码，将号码存入HashMap中。

由于HashMap的存和取在不存在Hash冲突的情况下为O(1)复杂度，所以该算法时间复杂度为O(n)。虽然算法2在时间复杂度上大大优于算法1，但是由于HashMap数据结构占用空间较大，如果15亿个号码都不重复，需存入HashMap中，仅考虑HashMap内数组存储的15亿个Entry的Key需占用空间同样为57220G，再加上存储的15亿个value，空间占用都肯定大于5.59G。

算法3：BitMap解法

我们先把问题简化，15亿个号码简化为10个10以内的号码去重，假设号码分别是

1, 2, 3, 4, 1, 3, 9, 8, 7, 6

我们使用BitMap来标记每个数字是否存在，

BitMap初始化使用一个10位的Bit数组，各位都初始化为0，    则

BitMap为  0000000000

数字1, 取BitMap第1位的值，为0, 表示1不存在重复的值，将BitMap第1位标记为1，则BitMap为 0000000001

数字2, 取BitMap第2位的值，为0，表示2不存在重复的值，将BitMap第2位标记为1，则BitMap为 0000000011

数字3，取BitMap第3位的值，为0，表示3不存在重复的值，将BitMap第3位标记为1，则BitMap为 0000000111

数字4，取BitMap第4位的值，为0，表示4不存在重复的值，将BitMap第4位标记为1，则BitMap为 0000001111

数字1，取BitMap第1位的值，为1，表示1存在重复的值，不标记BitMap，则

BitMap为 0000001111

数字3，取BitMap第3位的值，为1，表示2存在重复的值，  不标记BitMap，则

BitMap为 0000001111

数字9，取BitMap第9位的值，为0，表示9不存在重复的值， 将BitMap第9位标记为1，则BitMap为 0100001111

数字8，取BitMap第8位的值，为0，表示8不存在重复的值， 将BitMap第8位标记为1，则BitMap为 0110001111

数字7，取BitMap第8位的值，为0，表示7不存在重复的值， 将BitMap第7位标记为1，则BitMap为 0111001111

数字6，取BitMap第8位的值，为0，表示6不存在重复的值， 将BitMap第6位标记为1，则BitMap为 0111101111

最终BitMap为0111101111

遍历BitMap的各位，如果该位为1，则表明存在数值为该位位数的数值，这样可以得到去重后的所有数值

为 9,8,7,6,4,3,2,1

该方法推广到15亿个号码去重，则使用的BitMap为15亿位，算法时间复杂度同样为O(n), 占用空间约等于15亿个bit约等于174.62M

可以看出，BitMap在大数据量，重复度不高的数值去重场景的空间占用方面有比较大的优势。

如果数值的重复度比较高,例如存在99.99%的重复，BitMap依然要占用15亿*100%个bit的空间，

而HashMap仅存储不重复的数值，则HashMap解法占用空间将变为原空间的0.01%

这种情况下BitMap与HashMap的空间占用优劣势就需要重新进行衡量。

牛顿迭代法求平方根

发表评论

如果暴力法求2的平方根，应该是二分查找，不断的用中点的平方与2进行对比，然后根据对比结果改变查找结果的范围。

这种方法如果要求精确度比较高的时候，查找的次数将非常可观。该算法暂且不在本文讨论。

本文要讨论的是一种可以快速求解函数零点的算法-牛顿迭代，可以用在求2的平方根上。

此牛顿即科学之父，艾萨克·牛顿。

求2的平方根，其实就是求 f(x) = x² – 2函数，当f(x)=0时x的解。

如何找到这个x的值，在牛顿迭代算法中的方法是随机选择曲线f(x)上的一个点。

假设第一个选取的是(x₀, y₀) = (4, 14)。

【图1】

如图1可以看出该点的切线与x轴的交点(x₁, 0)是一个更加接近(x, 0)的值。

那么如何求x₁的值，我们需要求切线的函数。

切线是一条直线，已知该切线经过(x₀, y₀)，(x₁, 0)两点，且切线的斜率为2x₀(斜率的推导先搁置，文末会详细推导)。

所以，可得

0-y₀ = (x₁ – x₀)*2x₀

x₁ = x₀ – y₀/(2x₀) 

x₁= x₀ – (x₀² – 2)/2x₀

因为x₀=4, 所以x₁= 4 – 14/(2*4) = 2.25

【图2】

如图2

在(x₁, 0)作一条垂直x轴的直线与f(x)曲线的交点为(x₁, y₁)，

则(x₁, y₁)点的切线与x轴的交点为(x₂, 0)。

(x₂, y₂)点的切线与x轴的交点为(x₃, 0)。

(x₃, y₃)点的切线与x轴的交点为(x₄, 0)。

……

所以整个迭代过程如下：

x₀=4.0000000000

x₁=2.2500000000

x₂=1.5694444444

x₃=1.4218903638

x₄=1.4142342859

x₅=1.4142135625

x₆=1.4142135624

……

随着不断迭代，切线交点不断向x接近，最终可以得到一个x的近似值，当达到一定的精确度之后，迭代停止。

此迭代思路亦可应用于其他函数零点的求解中，只需改变对应的曲线和切线的函数即可。

Java代码实现，递归实现

public class Newton { public static void main(String[] args) { double x = newton(2); } private static double newton(double x) { if (Math.abs(x * x - 2) > 0.0000000001) { // 精确度达到小数点后10位停止迭代 return newton(x - (x * x - 2) / (2 * x)); } else { return x; } } }

附录

f(x) = x² – 2 函数曲线的切线斜率的推导

需要使用微积分的思维

我们知道曲线上两点(x₀, y₀)(x₁, y₁)连线的斜率的求解方法为

(y₀-y₁)/(x₀ – x₁)

y₀=x₀² – 2

y₁=x₁² – 2

代入斜率计算公式 = ((x₀² – 2) – (x₁² – 2))/(x₀ – x₁) 

=(x₀² – x₁²)/(x₀ – x1) 

=(x₀ – x₁)*(x₀ + x₁)/(x₀ – x₁)

 =x₀ + x₁

【图3】

当(x₀, y₀)(x₁, y₁)无限接近(x, y)时的直线的斜率即为该点的切线斜率

lim(x₀ + x₁) = 2x

可求得点(x, y)的切线斜率 = 2x